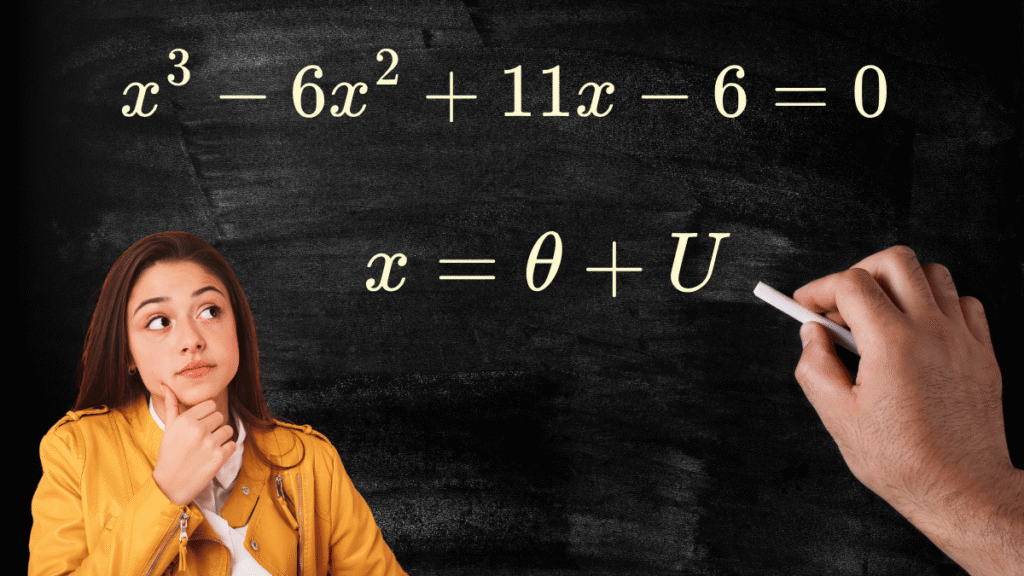Neste post vamos resolver a equação \(3x−5 = \sqrt{x} \) usando o método SAAMM, procurando uma raiz \(x \) no intervalo entre 0 e 5.
Vamos explicar detalhadamente o método para que possam apreciar.
O método que vamos usar para resolver equações transcendentais como esta se baseia em quatro passos:
Passo 1: Substituição
Substituição inicial: Substituímos \(x=θ+U\), onde \(U\) é o chute inicial e \(θ\) representa um valor pequeno.
Passo 2: Uso da Calculadora de Taylor
Se a equação que queremos encontrar a raiz, possuir funções transcendentais, escrevemos as funções aproximadas das funções transcendentais, seguindo a Regra 2, para cada uma das funções transcendentais presentes:
Regra 2:
Substituímos, cada uma das funções transcendentais presentes, por uma função transcendental aproximada representada pela aproximação de Taylor de primeira ordem, em torno de U, da seguinte forma (A Calculadora de Taylor):
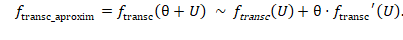
A função \(\sqrt{x}\) será expandida em Série de Taylor em torno de U: $$\sqrt{x} = \sqrt{\theta + U}. $$
Usando a Série de Taylor até a primeira ordem: $$\sqrt{\theta + U} \approx \sqrt{U} + \frac{\theta}{2\sqrt{U}}. $$.
Aqui, definimos: $$S = \frac{1}{2\sqrt{U}} \quad \text{e} \quad T = \sqrt{U} ,$$ resultando em: $$\sqrt{\theta + U} \approx T + \theta S. $$.
Substituímos \(x = \theta + U \) e a expansão de \(\sqrt{x}\) na equação \(3x – 5 = \sqrt{x}: \) $$ 3(\theta + U) – 5 = T + \theta S. $$ Rearranjando os termos: $$3\theta + 3U – 5 = T + \theta S.$$
Passo 3: Linearização em θ
Na linearização, somente consideramos na equação os termos ate primeira ordem em \(\theta\).
Isolamos os termos lineares em \(\theta:\) $$(3−S)θ=T−3U+5. $$
Assim, \(θ\) é dado por: $$ \theta = \frac{T – 3U + 5}{3 – S}.$$
Passo 4: Determinação do chute inicial U
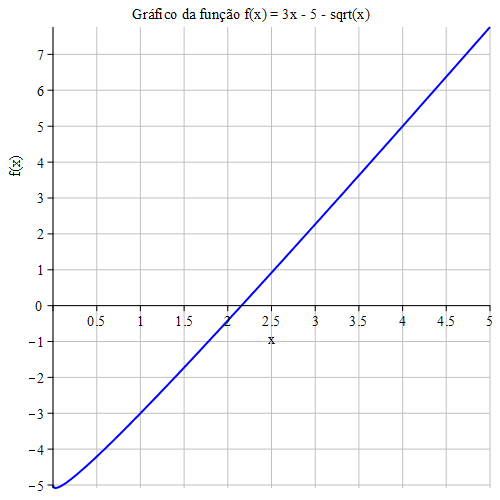
Neste passo, utilizamos o método gráfico para encontrar uma estimativa inicial para \(U\). Traçamos, em um mesmo gráfico, a função (ou as funções) envolvidas, procurando o ponto de interseção entre a curva e o eixo \(x\), ou entre duas funções. Esse ponto de interseção fornece o valor aproximado de \(U\), que será usado para determinar a solução aproximada da equação original.
Uma vez obtido o valor de \(U\), voltamos à forma original \(x = \theta + U\) para calcular a estimativa final. O valor de \(U\) — que serve como ponto de referência — é obtido por análise gráfica, identificando aproximadamente onde a função cruza o eixo horizontal. Esse processo torna o método intuitivo e visual, ideal para estudantes e iniciantes.
Usamos \(U\) como chute inicial. Aqui, escolhemos \(U = 2\) (um valor aproximado no intervalo dado).
- Para \(U=2 \):
- \(T = \sqrt{U} = \sqrt{2} \approx 1.414\),
- \(S = \frac{1}{2\sqrt{U}} = \frac{1}{2\sqrt{2}} \approx 0.354\).
- Substituímos em \(\theta:\) $$\theta = \frac{1.414 – 3(2) + 5}{3 – 0.354}.$$Calculando:$$\theta = \frac{1.414 – 6 + 5}{2.646} = \frac{0.414}{2.646} \approx 0.156.$$
- Finalmente, encontramos: $$x = \theta + U = 0.156 + 2 = 2.156.$$
Cálculo do Erro Relativo
Para verificar a precisão da solução, usamos métodos numéricos para encontrar o valor exato de \(x\). A solução exata da equação \(3x – 5 = \sqrt{x}\) é aproximadamente \(x_{\text{exato}} \approx 2.162.\)
O erro relativo é dado por: $$\text{Erro relativo} = \frac{|x_{\text{exato}} – x|}{x_{\text{exato}}} \cdot 100\%.$$
Substituindo os valores: $$\text{Erro relativo} = \frac{|2.162 – 2.156|}{2.162} \cdot 100 \approx 0.28\%.$$
Passos Realizados no Código Python
Para resolver a equação \(3x – 5 = \sqrt{x}\) no intervalo de x entre 0 e 5 utilizando o método SAAMM, e esboçar o gráfico correspondente, você pode utilizar o seguinte código em Python:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
# Definindo a função
def func(x):
return 3*x - 5 - np.sqrt(x)
# Estimativa inicial para a raiz
x0 = 2.0
# Encontrando a raiz usando fsolve
root = fsolve(func, x0)[0]
# Calculando o erro relativo
erro_relativo = abs((root - x0) / root) * 100
# Gerando valores de x para o gráfico
x_values = np.linspace(0, 5, 400)
y_values = func(x_values)
# Plotando o gráfico
plt.figure(figsize=(10, 6))
plt.plot(x_values, y_values, label=r'$3x - 5 - \sqrt{x}$')
plt.axhline(0, color='gray', linestyle='--')
plt.axvline(root, color='red', linestyle='--', label=f'Raiz aproximada: x = {root:.4f}')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gráfico da função $3x - 5 - \sqrt{x}$')
plt.legend()
plt.grid(True)
plt.show()
# Exibindo a raiz e o erro relativo
print(f'Raiz aproximada: x = {root:.4f}')
print(f'Erro relativo: {erro_relativo:.2f}%')
Explicação do Código:
- Definição da Função:
A funçãofunc(x)representa a equação \(3x – 5 – \sqrt{x} \). Nosso objetivo é encontrar o valor de \(x\) que satisfaz essa equação. - Estimativa Inicial:
\(U=2 \)é a estimativa inicial para a raiz. Neste caso, escolhemos 2.0, mas você pode ajustar conforme necessário. - Encontrando a Raiz:
Utilizamosfsolvedo SciPy para encontrar a raiz da função.fsolveé uma função numérica que encontra as raízes de uma função não-linear. - Calculando o Erro Relativo:
O erro relativo é calculado para avaliar a precisão da estimativa da raiz. É dado por: $$\text{Erro Relativo} = \left| \frac{\text{raiz} – x0}{\text{raiz}} \right| \times 100\%$$ - Gerando Valores para o Gráfico:
x_valuesé um array de valores de \(x\) no intervalo de 0 a 5.y_valuessão os valores correspondentes da funçãofunc(x). - Plotando o Gráfico:
Utilizamos Matplotlib para plotar o gráfico da função. A linha horizontal em \(y=0\) e a linha vertical na raiz aproximada são adicionadas para referência visual. - Exibindo Resultados:
O código imprime a raiz aproximada e o erro relativo no console.
Nota: Este código utiliza bibliotecas populares como NumPy, SciPy e Matplotlib. Certifique-se de tê-las instaladas no seu ambiente Python. Você pode instalá-las usando pip:
pip install numpy scipy matplotlib
Este método analítico aproximado é útil em diversas situações e serve como preparação para cursos mais avançados de cálculo e métodos numéricos.
Passos Realizados no Código Maple
Se o leitor preferir explorar uma solução usando Maple, aqui está o código correspondente para resolver a equação \(3x – 5 = \sqrt{x}\), plotar o gráfico da função, e calcular o erro relativo:
# Definição da função
f := x -> 3*x - 5 - sqrt(x):
# Encontrando a raiz da equação no intervalo [0, 5]
raiz := fsolve(f(x) = 0, x = 0..5);
# Cálculo do erro relativo baseado em uma estimativa inicial (por exemplo, x0 = 2.0)
x0 := 2.0:
erro_relativo := abs((raiz - x0)/raiz) * 100;
# Gerando o gráfico da função
with(plots):
plot(f(x), x = 0..5, color = blue, thickness = 2, title = "Gráfico da função 3x - 5 - sqrt(x)", labels = ["x", "f(x)"], legend = "3x - 5 - sqrt(x)"):
Explicação do código:
- Definição da Função:
A função \(f(x) = 3x – 5 – \sqrt{x}\) é definida comf := x -> 3*x - 5 - sqrt(x). - Resolução da Equação:
O comandofsolveencontra a raiz da equação no intervalo [0,5]. O resultado é armazenado na variávelraiz. - Cálculo do Erro Relativo:
O erro relativo é calculado com base em uma estimativa inicial x0=2.0x_0 = 2.0×0=2.0, usando a fórmula: Erro Relativo=∣raiz−x0raiz∣×100%\text{Erro Relativo} = \left| \frac{\text{raiz} – x_0}{\text{raiz}} \right| \times 100\%Erro Relativo=raizraiz−x0×100% - Plotagem do Gráfico:
O gráfico da função \(f(x) = 3x – 5 – \sqrt{x}\) no intervalo [0,5] é gerado com o comandoplotdo pacoteplots.
Conclusão
Usando o método SAAMM, encontramos a solução aproximada \(x \approx 2.156\) para a equação \(3x – 5 = \sqrt{x}\), com um erro relativo de apenas 0.28%. Isso demonstra a eficiência do método para resolver equações transcendentais de forma analítica e simplificada.
A vantagem desse método é que podemos repetir o processo indefinidamente quantas vezes acharmos necessário, fazendo com que a última resposta seja o chute inicial, gerando um valor cada vez mais preciso.
Vitrine dos nossos Livros
Visite nosso Blog
De Lâmpadas a Gás à Automação: A Eterna Dança da “Destruição Criativa” no Mercado de Trabalho
A imagem mostra uma imagem pictórica de um anúncio antigo da Union Carbide Gás, que…
📘 Resolvendo com SAAMM a equação cúbica: $$x^3 – 6x^2 + 11x – 6 = 0 $$
O lugar de cada coisa: Homem x Máquina
Na ciência e na engenharia, estamos cercados por equações que precisam ser resolvidas. Mas nem…
Qual a previsão da IA daqui a uma década na vida das pessoas?
A Inteligência Artificial (IA) está evoluindo rapidamente e, em 10 anos, é provável que ela…
A IA é apenas o piano
A IA é apenas uma tecnologia poderosa, mas, como qualquer ferramenta, seu impacto depende de…
“Download” de Conhecimento: Um Mito da Era Digital
É comum que as pessoas confundam o poder computacional das máquinas com a agilidade do…