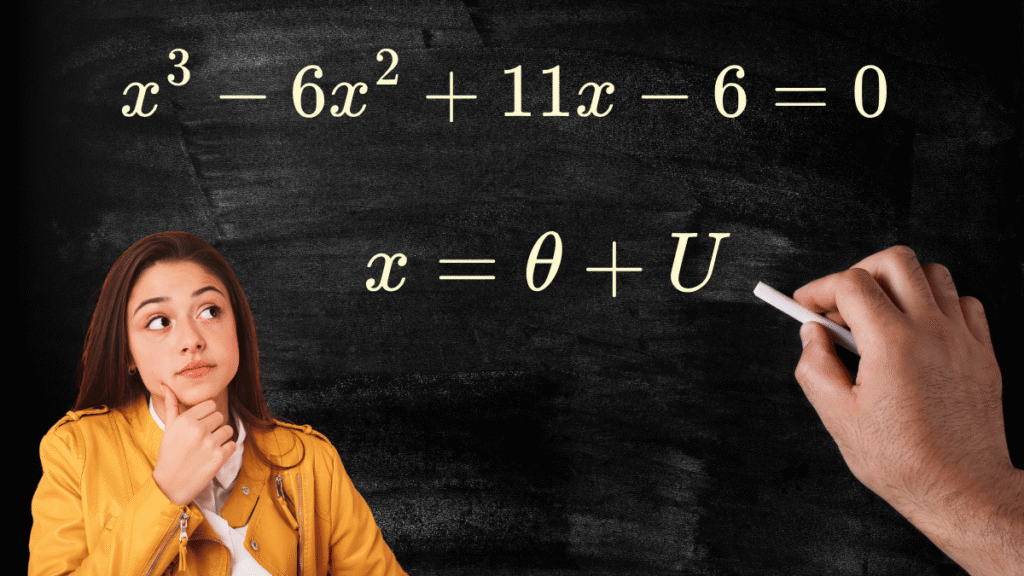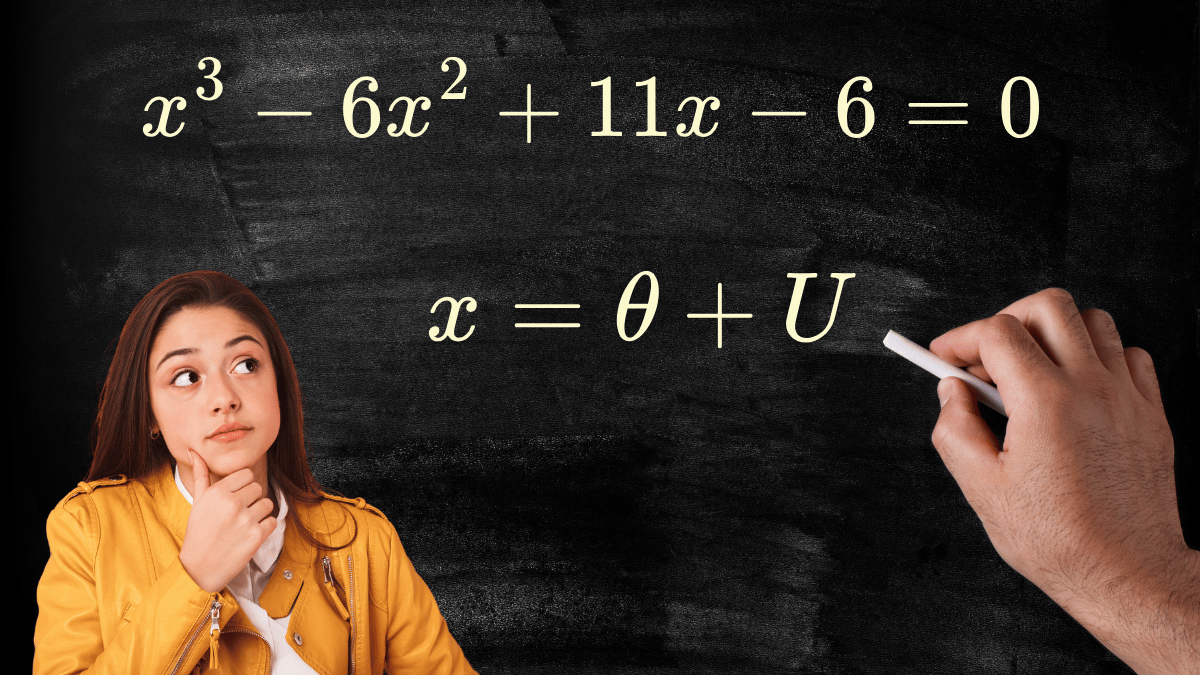
Resolução de uma Equação Cúbica $$x^3 – 6x^2 + 11x – 6 = 0 $$
Aprenda a aplicar o método SAAMM na resolução aproximada de equações algébricas de grau 3.
Este é um dos destaques da Aula 8 do curso Pensando Fora da Caixa 1: Métodos Analíticos Aproximados para Resolver Equações Algébricas.
Equação proposta:
Considere a seguinte equação cúbica:
$$x^3 – 6x^2 + 11x – 6 = 0 $$
Vamos resolvê-la utilizando o método SAAMM, por meio da aplicação de seus três passos fundamentais.
📌 O que é o Método SAAMM?
O SAAMM (Simplified Approximate Analytical Mathematical Method) é uma metodologia inovadora que permite resolver equações algébricas — especialmente de grau superior — de forma aproximada, visual e acessível.
Ele é composto por três passos simples:
1-) Substituição da variável original;
2-) Linearização da equação transformada;
3-) Determinação gráfica do chute inicial U.
✅ Passo 1: Substituição de variável
Substituímos na equação original a variável \(x\) por: \(x = \theta + U \), e obtemos:
\( (\theta + U)^3 – 6(\theta + U)^2 + 11(\theta + U) – 6 = 0 \tag{1} \)
✅ Passo 2: Linearização em θ
À primeira vista, a substituição parece gerar uma expressão complexa devido às potências da variável. No entanto, utilizamos uma aproximação prática e eficiente baseada na suposição de que θ é pequeno. Para isso, aplicamos a seguinte regra de aproximação, válida quando \( \theta^2 \approx 0 \):
📐 Regra 1 – Expansões simplificadas:
Partindo de um processo de indução matemática, como o mostrado a seguir:
$$ (\theta + U)^2 = \theta^2 + 2\theta U + U^2 $$
$$ (\theta + U)^3 = \theta^3 + 3U\theta^2 + 3U^2\theta + U^3 $$
$$ (\theta + U)^4 = \theta^4 + 4U\theta^3 + 6U^2\theta^2 + 4U^3\theta + U^4 $$
Obtemos o seguinte resultado geral, para k um número inteiro:
$$ (\theta + U)^k \approx kU^{k-1}\theta + U^k $$
Aplicando a Regra 1 na Equação (1), obtemos:
$$ (\theta + U)^3 – 6(\theta + U)^2 + 11(\theta + U) – 6 = 0 $$
Expandindo e organizando:
$$ 3U^2\theta – 12U\theta + 11\theta + U^3 – 6U^2 + 11U – 6 = 0 $$
Agrupando termos:
$$ (3U^2 – 12U + 11)\theta = -U^3 + 6U^2 – 11U + 6 $$
Logo, a solução aproximada para θ é:
$$ \theta = \frac{-U^3 + 6U^2 – 11U + 6}{3U^2 – 12U + 11}$$
Como \(x = \theta + U \), obtemos:
$$ x = \frac{-U^3 + 6U^2 – 11U + 6}{3U^2 – 12U + 11} + U $$
Após simplificação algébrica, a expressão final é:
$$ x = \frac{2U^3 – 6U^2 + 6}{3U^2 – 12U + 11} \tag{2} $$
✅ Passo 3: Determinação de U com o método gráfico
Agora queremos encontrar U para substituir na Eq. (2) e encontrar x.
Uma das possibilidades de se fazer isso, não única, mas uma delas, para encontrar um valor adequado para U, consiste em quebrar a equação original,
$$x^3 – 6x^2 – 11x + 6 = 0 $$
de uma forma adequada para se obter duas curvas. Assim, separamos a equação em dois lados:
- Lado esquerdo: \( f_{\text{esq}}(x) = x^3 \)
- Lado direito: \( f_{\text{dir}}(x) = 6x^2 – 11x + 6 \)
Traçando os gráficos dessas duas funções (em softwares como Python, Maple, MATLAB, ou até mesmo à mão), os pontos de interseção entre \( f_{\text{esq}}\) e \( f_{\text{dir}}\) nos darão possibilidade de arbitrar os valores de U. Como se trata de uma equação cúbica, espera-se encontrar até três pontos de interseção, ou seja, três raízes reais, neste problema específico, como podemos ver na Figura 1.
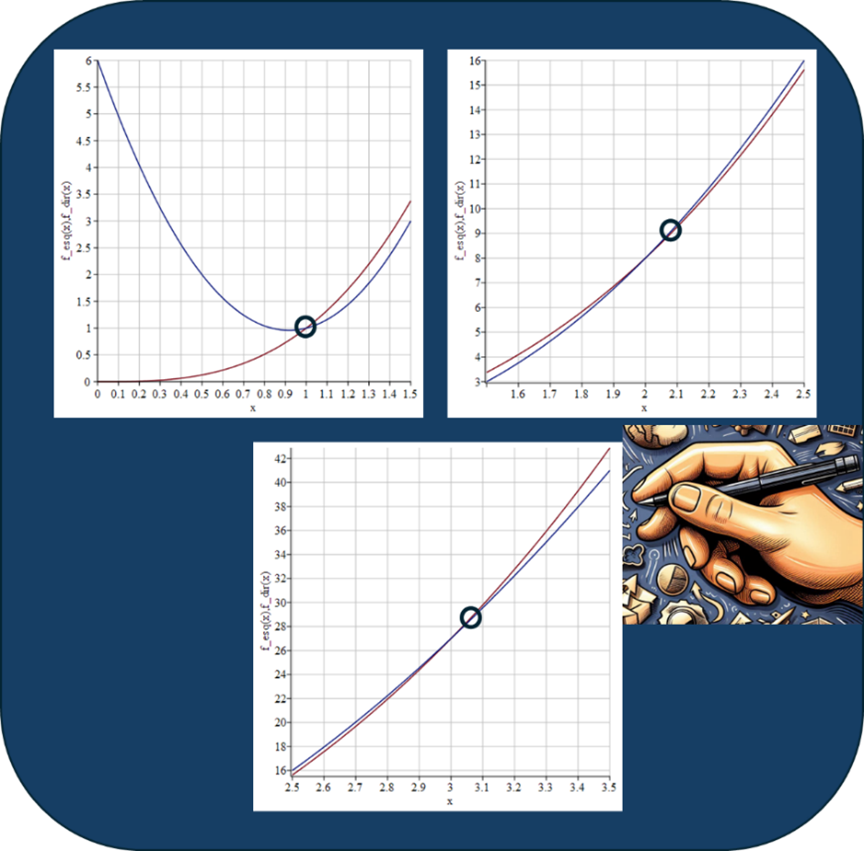
Figura 1 – Gráficos das interseções das funções, \( f_{\text{esq}}\) e \( f_{\text{dir}}\), resultando em três pontos de interseção que podem ser considerados uma boa estimativa de chute inicial para U. Observando-se os gráficos, podemos arbitrar, U1=1.1, U2=2.2 e U3=3.2, como possíveis chutes iniciais para determinar as raízes.
Após plotar os gráficos, você observará três interseções. Suponha que, olhando o gráfico, escolhemos: U1=1.1, U2=2.2 e U3=3.2, como chutes iniciais para determinar as raizes.
📊 Supondo os valores de U estimados graficamente:
Após plotar os gráficos, você observará três interseções. Suponha que, olhando o gráfico, escolhemos: U1=1.1, U2=2.2 e U3=3.2, como chutes iniciais para determinar as raízes.
- \(U_1 = 1{,}1 \)
- \(U_2 = 2{,}2 \)
- \(U_3 = 3{,}2 \)
Aplicando cada valor de U na Equação (2), obtemos os valores aproximados de x, para as três raízes possíveis:
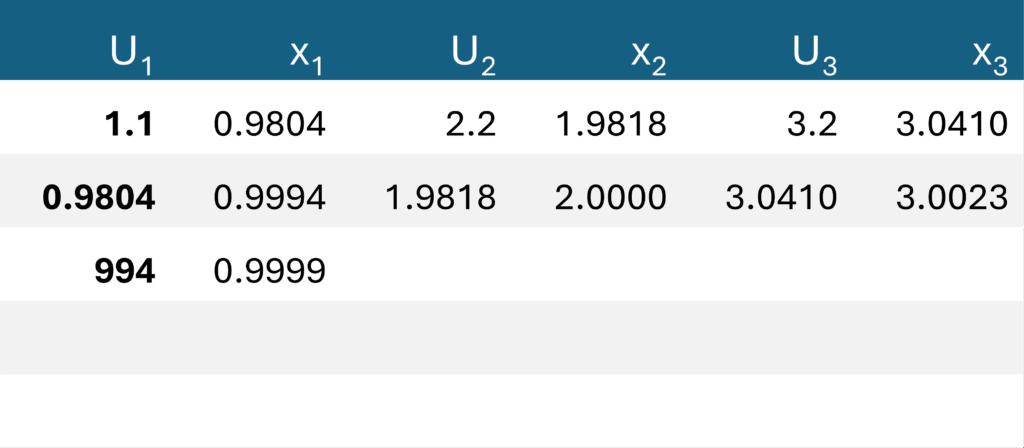
Se aplicarmos esses valores de x na equação original $$ x^3 – 6x^2 + 11x – 6=0, $$ verificamos que os resíduos (diferenças) são muito próximos de zero, o que confirma a qualidade da aproximação fornecida pelo método SAAMM.
✅ Conclusão
O método SAAMM oferece uma alternativa analítica poderosa para resolver equações cúbicas com simplicidade e intuição. A substituição, a linearização e o uso de gráficos tornam o processo acessível para estudantes e professores que desejam ir além dos métodos numéricos convencionais.
🔗 Quer aprender mais?
📺 Assista à Aula 8 do curso Pensando Fora da Caixa no YouTube
📘 Veja também: Aula 7 – Qual É O SEGREDO Para Melhorar Seus Resultados em Matemática?
🔬 Conheça nosso site: CONHEÇA O MÉTODO SAAMM
Vitrine dos nossos Livros
De Lâmpadas a Gás à Automação: A Eterna Dança da “Destruição Criativa” no Mercado de Trabalho
De Lâmpadas a Gás à Automação: A Eterna Dança da “Destruição Criativa” no Mercado de…
📘 Resolvendo com SAAMM a equação cúbica: $$x^3 – 6x^2 + 11x – 6 = 0 $$
O lugar de cada coisa: Homem x Máquina
Na ciência e na engenharia, estamos cercados por equações que precisam ser resolvidas. Mas nem…
Qual a previsão da IA daqui a uma década na vida das pessoas?
A Inteligência Artificial (IA) está evoluindo rapidamente e, em 10 anos, é provável que ela…
A IA é apenas o piano
A IA é apenas uma tecnologia poderosa, mas, como qualquer ferramenta, seu impacto depende de…
“Download” de Conhecimento: Um Mito da Era Digital
“Download” de Conhecimento: Um Mito da Era Digital Capacidade de Processamento: É comum que as…