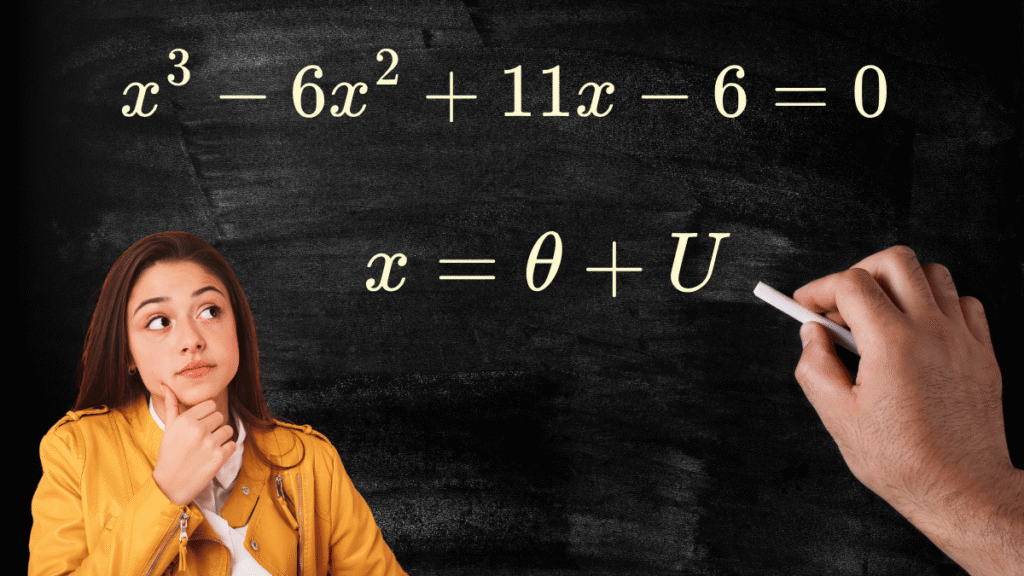Nota Histórica: A gênese e evolução do Método SAAMM

O Método SAAMM — Simplified Approximate Analytical Mathematical Method não surgiu de forma súbita, mas como resultado de um processo contínuo de amadurecimento conceitual e metodológico ao longo de quase uma década de pesquisas.
Suas origens remontam às primeiras tentativas de se obter soluções analíticas fechadas para equações transcendentais e diferenciais complexas — especialmente aquelas que descrevem fenômenos quânticos e eletrônicos em dispositivos de nanoescala.

O primeiro embrião do SAAMM pode ser identificado no trabalho de 2016, intitulado “An Explicit Quantum-Mechanical Compact Model for the I–V Characteristics of Cylindrical Nanowire MOSFETs” (IEEE Transactions on Nanotechnology) [1].
Naquele estudo, foi proposta uma abordagem analítica para o acoplamento entre as equações de Poisson e Schrödinger em geometria cilíndrica, com o objetivo de descrever o potencial quântico e as características de corrente de nanofios semicondutores.
Ainda que sem nomear explicitamente o método, o artigo introduzia a essência do que viria a se tornar o SAAMM: a ideia de linearizar funções não lineares complexas em torno de pontos de referência, utilizando aproximações parabólicas locais e substituições analíticas controladas.
Essas aproximações permitiram transformar equações transcendentais em expressões polinomiais resolvidas simbolicamente, garantindo simultaneamente clareza física e consistência matemática — características que se tornariam marca registrada do método.

O segundo marco evolutivo ocorreu no artigo de 2019, “Fully Analytical Compact Model for the I–V Characteristics of Large-Radius Junctionless Nanowire FETs” (IEEE Transactions on Nanotechnology) [2].
Nesse trabalho, foi introduzido o chamado Function Mapping Method (FMM), uma técnica inovadora que substituía funções transcendentais, como o logaritmo natural, por funções analíticas aproximadas de segunda ordem, preservando a continuidade entre os regimes de operação do dispositivo.
Embora apresentado sob outro nome, o FMM representava uma aplicação direta dos princípios do SAAMM:
a substituição de funções complexas por aproximações locais obtidas via expansão de Taylor, e a reorganização simbólica da equação resultante para obtenção de soluções explícitas.
O método de mapeamento funcional foi, em essência, a formalização inicial da “Calculadora de Taylor” — o segundo passo do SAAMM moderno.

O terceiro passo dessa trajetória consolidou-se em 2021, no artigo “Accurate and Fully Analytical Expressions for Quantum Energy Levels in Finite Quantum Wells” (Journal of Computational Electronics) [3].
Nesse estudo, voltado à determinação analítica dos níveis de energia de poços quânticos finitos, foi proposto o Simplified Cosine/Sine Model (SCSM), no qual funções trigonométricas transcendentes foram substituídas por suas aproximações parabólicas locais, obtendo-se expressões analíticas diretas para os autovalores.
Esse artigo marcou o momento em que o método adquiriu identidade independente, deixando de ser apenas uma ferramenta aplicada à microeletrônica para se tornar uma estratégia matemática de amplo alcance — generalizável a outros tipos de equações transcendentais e diferenciais não lineares.
O raciocínio do SCSM evoluiria naturalmente, poucos anos depois, para a formulação sistemática do SAAMM.

O quarto marco do desenvolvimento do método ocorreu em 2025, com a publicação do artigo “On approximate analytical solutions of transcendental equations” na Revista Brasileira de Ensino de Física (RBEF) [4].
Este trabalho representou a formalização definitiva do SAAMM, agora apresentado como um arcabouço matemático geral aplicável a diferentes contextos da ciência e da engenharia.
Nele, o método foi sistematizado em três passos fundamentais:

1. Substituição analítica inicial, que introduz um ponto de referência U para a análise local da função;
2. Aproximação analítica controlada, obtida por expansão de Taylor até a ordem desejada (linear, parabólica, etc.), constituindo a “Calculadora de Taylor”;
3. Reorganização simbólica e determinação da solução analítica aproximada, com possibilidade de refinamento progressivo via iterações sucessivas ou subdivisão do domínio — a chamada técnica do “U partido”.

O artigo da RBEF trouxe também três aplicações canônicas — o circuito resistor–diodo, o nanofio semicondutor e o pêndulo simples — evidenciando a versatilidade e poder unificador do SAAMM.
Esses exemplos mostraram que o método não apenas gera soluções analíticas aproximadas com erro controlado, mas também permite compreensão visual e física do comportamento das funções transcendentais envolvidas.
Além disso, a publicação destacou o papel do SAAMM como ponte pedagógica entre o cálculo simbólico e o numérico, sendo especialmente adequado ao ensino de métodos analíticos aproximados em disciplinas de física matemática e cálculo numérico.

Por fim, entre 2023 e 2025, o método atingiu maturidade e foi definitivamente consolidado sob o nome SAAMM — Simplified Approximate Analytical Mathematical Method, incorporando todos os elementos que hoje o caracterizam:

• a substituição analítica e o ponto de referência U;
• a Calculadora de Taylor;
• a linearização simbólica e obtenção de soluções aproximadas com erro mensurável;
• e a técnica do U partido, que garante precisão progressiva sem perda de interpretabilidade.

A aplicação do SAAMM a problemas clássicos de física e engenharia — como o pêndulo simples em grandes amplitudes e o poço quântico finito — mostrou que o método não é apenas uma ferramenta de cálculo, mas um arcabouço conceitual robusto, que promove uma compreensão analítica profunda do comportamento das funções transcendentais.
Sua principal força está em conciliar clareza simbólica, precisão controlada e valor didático, servindo tanto à pesquisa científica quanto ao ensino de métodos analíticos avançados.

Dessa forma, o SAAMM pode ser visto como o produto natural de uma linha de pesquisa coerente e progressiva, iniciada em 2016 e consolidada ao longo dos anos seguintes.
Ele representa a maturação de uma visão científica que busca compreender — e não apenas numericamente resolver — os fenômenos descritos por equações transcendentais e diferenciais, reafirmando o valor das soluções analíticas aproximadas na ciência contemporânea.