Você já se deparou com equações transcendentais do tipo:
$$2x – 7=sin(x),$$
e ficou em dúvida sobre como resolvê-las de forma simples e rápida?

Neste blog, apresentaremos uma abordagem eficiente usando o Método SAAMM, uma técnica poderosa para a resolução aproximada de problemas complexos, muito ensinada em nossos livros, vídeos do YouTube e aqui em nosso blog.
Para acompanhar a resolução completa deste problema passo a passo, não deixe de conferir nosso vídeo no YouTube:
YouTube
👉 Resolvendo Equação Transcendental com SAAMM
Equações transcendentais são aquelas que envolvem funções não polinomiais, como trigonométricas, exponenciais ou logarítmicas, combinadas com termos algébricos.
Elas surgem naturalmente em problemas de física, engenharia e até na matemática aplicada. Desde os primeiros matemáticos da antiguidade até os dias de hoje, a busca por soluções dessas equações tem sido um desafio fascinante. A necessidade de aproximar raízes dessas equações levou ao desenvolvimento de métodos que tornam o processo mais simples e prático, como o SAAMM.
Vamos resolver a seguinte equação transcendental:
$$2x-7=sin(x)$$
A resolução se divide em quatro passos. Vamos explicar o passo a passo e a grande sacada do método SAAMM.
Passo 1: Substituição de \( x \) por \( x = \theta + U \)
+ Detalhes …
O primeiro passo do método SAAMM é a substituição da variável \(x\) pela soma de um número muito pequeno \(\theta\) (quanto menor, melhor a aproximação) e uma nova variável \(U\) , onde: $$x = θ + U.$$
Essa substituição é fundamental porque permite “quebrar” o problema em duas partes: uma parte controlada e linear em função de \(θ\) e outra que será ajustada posteriormente com a escolha de um chute inicial, \(U\).
Passo 2 e Passo 3: Uso da Calculadora de Taylor e Linearização em θ
+ Detalhes …
Ao substituir \(x = θ + U\), todas as funções transcendentais (como \(sin(x)\)) devem ser expandidas em séries de Taylor com respeito a \(θ\) e não a \(x\).
Essa é a grande sacada do método SAAMM!
Expandir em \(θ\) e não em \(x\), e aproveitar todas as consequências dessa ação.(R. RAGI)
A expansão em Série de Taylor deve considerar os termos até primeira ordem em \(θ\). Neste passo, devemos manter na equação apenas os termos de \(θ\) de ordem menor ou igual a um, e desprezar todos os demais.
Para a nossa equação, substituímos o termo \(sin(x)\) pela função aproximada, dada pelo resultado que chamamos de Regra 2 ou Calculaadora de Taylor:
$$f_{aprox} ( θ + U ) = f ( U ) + θ . \frac{df(x)}{dx}|_{( x=U )}$$
Para o caso do \(sin(x)\), ficamos com:
$$f_{aprox} ( θ + U ) = sin( U ) + θ . cos( U )$$
Aqui, chamamos, \(S = cos(U)\) e \(T = sin(U)\), assim, a função aproximada, \( f_{aprox} \), de \(sin(x)\), pode ser escrita como:
$$ sin(x) ≈ f_{aprox} ( θ + U ) = T + θ . S. $$
Substituímos esse resultado agora na equação original:
$$2x−7 = sin(x),$$
de onde obtemos,
$$ 2(θ + U) − 7 = S θ + T. $$
Manipulando os termos, podemos isolar θ, e obter:
$$ θ = \frac{ 7 – 2U + T }{ 2 – S } $$
Por último, encontramos o valor de x, considerando, \(x = θ + U\), resultando em:
$$x = \frac{ SU – 7 – T }{S – 2 }$$
Passo 3: Encontrar U através da intersecção entre as curvas mostradas na Figura 1.
+ Detalhes …
Mas como encontramos U?
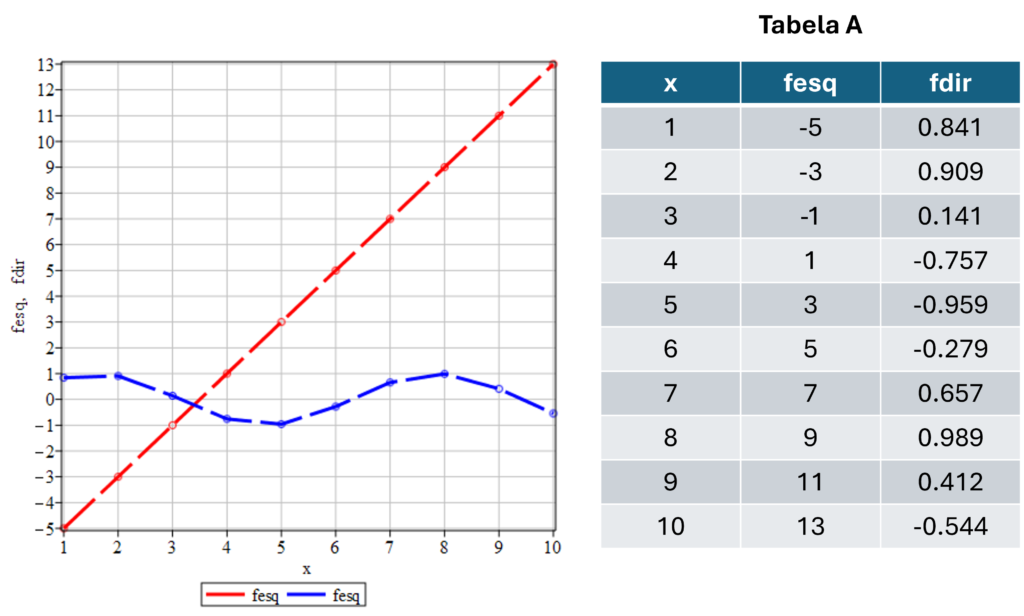
Esse é o momento do esboço gráfico! Esboçamos a função do lado esquerdo da equação original, fesq(x) = 2x−7, contraposta com a função do lado direito, fdir(x) = sin(x), em um único gráfico e escolhemos grosseiramente um valor inicial para U, a partir do ponto de intersecção entre essas duas curvas.
O gráfico das duas curvas, fesq(x) e fdir(x), contrapostos, pode ser visto na Figura 1, obtido muito facilmente, no Maplesoft, a partir do levantamento da Tabela A, no intervalo para x, 1 <= x <= 10. Alternativamente, esse gráfico pode ser obtido no Python, com o código abaixo.
O levantamento da Tabela A, permite esboçarmos as curvas mostradas na Figura 1. A intersecção entre essas curvas é o chute inicial, U.
Código Python –>>
import numpy as np
import matplotlib.pyplot as plt
# Definindo o intervalo
x = np.linspace(1, 10, 100)
# Funções: Lado esquerdo (2x - 7) e lado direito (sin(x))
fesq = 2 * x - 7
fdir = np.sin(x)
# Criando o gráfico
plt.figure(figsize=(8, 6))
plt.plot(x, fesq, 'r--o', label="fesq (2x - 7)", linewidth=2, markersize=5)
plt.plot(x, fdir, 'b--o', label="fdir (sin(x))", linewidth=2, markersize=5)
# Adicionando grade, legendas e rótulos
plt.axhline(0, color='gray', linewidth=0.8, linestyle='--')
plt.axvline(0, color='gray', linewidth=0.8, linestyle='--')
plt.grid(color='gray', linestyle='--', linewidth=0.5, alpha=0.7)
plt.legend()
plt.xlabel("x")
plt.ylabel("fesq, fdir")
plt.title("Gráfico de 2x - 7 e sin(x)")
plt.show()
Note que, para rodar o programa em Python acima é necessário que a biblioteca NumPy, esteja instalada no ambiente Python que você está usando. Analogamente, a biblioteca Matplotlib para a criação de gráficos, também precisa estar instalada para que o programa execute corretamente.
A partir da análise gráfica da Figura 1, podemos estimar o valor de U, o qual escolhermos, aproximadamente, U = 3.5.
Usando esse valor de U na expressão de x encontrada acima:
$$x = \frac{ SU – 7 – T }{S – 2 }$$
obtemos: $$ x_{SAAMM} = 3.3805$$
O método SAAMM contribui para o desenvolvimento do pensamento analítico, pois incentiva a busca por soluções criativas, estimula a abstração e a generalização, promove a decomposição de problemas complexos, desenvolve o raciocínio lógico e sequencial, e fortalece a capacidade de avaliar resultados.
Análise dos resultados
Ao resolvermos numericamente a equação transcendental,
+ Detalhes…
$$2x−7=sin(x)$$
com o auxílio de ferramentas como Maple ou Python, encontramos um valor de referência, preciso, para x, dado por:
$$x_{REF}:=3.381293824$$
Esse valor pode ser calculado utilizando métodos numéricos precisos ou soluções simbólicas disponíveis em plataformas computacionais.
Cálculo do Erro Relativo
+ Detalhes…
Se compararmos o valor obtido pelo método SAAMM com o valor de referência xREF, podemos calcular o erro relativo, da seguinte forma:
$$Erro_{Relativo} = \frac{ ∣ x_{SAAMM} − x_{REF} ∣ }{ x_{REF}} \times 100 \ (\%) $$
Para este caso específico, o erro relativo é 0.02%, demonstrando que o método SAAMM fornece resultados extremamente próximos aos valores exatos, o que o torna uma excelente abordagem para finalidades práticas, mesmo com poucas iterações.
Maple x Python: Discussão Final
+ Detalhes …
Resolução no Maple
- Praticidade e foco matemático: Maple é projetado para lidar com problemas matemáticos simbólicos e numéricos com facilidade. Resolver equações transcendentais ou obter valores precisos, como xREF, requer poucas linhas de código.
- Ideal para ensino e análise teórica: Com uma interface gráfica rica, o Maple permite aos usuários visualizar cálculos, gráficos e manipulações matemáticas diretamente, tornando-o mais acessível para iniciantes.
- Limitação: É uma ferramenta proprietária, o que pode limitar seu acesso a quem não possui licença.
Resolução no Python
- Flexibilidade e integração: Python é uma linguagem de propósito geral que, com bibliotecas como SymPy e SciPy, permite resolver equações transcendentais com eficiência. Além disso, Python é ideal para automação, integração com sistemas maiores e análise de dados.
- Acessibilidade: Por ser gratuito e amplamente utilizado, Python oferece uma alternativa economicamente viável para estudantes e pesquisadores.
- Curva de aprendizado: Embora seja mais poderoso para integração, Python exige maior conhecimento de programação e bibliotecas, o que pode ser uma barreira inicial.
Recomendação
Python: Melhor para quem busca flexibilidade, integração com outras áreas (como desenvolvimento de aplicativos ou análise de dados) ou uma alternativa gratuita. Ideal para pesquisadores e estudantes que já possuem alguma familiaridade com programação.
Maple: Ideal para quem deseja uma ferramenta focada em matemática, com visualização integrada e facilidade para manipular equações simbólicas e gráficos. Recomendado para o ensino do método SAAMM e cálculos teóricos.
Ambas as ferramentas são capazes de resolver a equação transcendental apresentada com alta precisão, e a escolha entre elas depende do contexto e das necessidades específicas do usuário.
Código Python completo (incluindo cálculo de erro relativo) –>>
import numpy as np
import matplotlib.pyplot as plt
# Funções para os dois lados da equação
def f_esq(x):
return 2 * x - 7
def f_dir(x):
return np.sin(x)
# Passo 1: Substituição e aproximação inicial
def expand_sin(theta, U):
S = np.cos(U)
T = np.sin(U)
return S * np.sin(theta) + T * np.cos(theta)
def solve_theta(U, theta_guess=0.01):
S = np.cos(U)
T = np.sin(U)
return (7 - 2 * U + T) / (2 - S)
# Passo 2: Ajuste gráfico para determinar U
x_vals = np.linspace(1, 10, 100)
fesq_vals = f_esq(x_vals)
fdir_vals = f_dir(x_vals)
# Esboço das curvas
plt.plot(x_vals, fesq_vals, label="2x - 7 (lado esquerdo)", color="red", linestyle="--")
plt.plot(x_vals, fdir_vals, label="sin(x) (lado direito)", color="blue", linestyle="-.")
plt.axhline(0, color="gray", linewidth=0.5)
plt.axvline(0, color="gray", linewidth=0.5)
plt.xlabel("x")
plt.ylabel("Valores das funções")
plt.legend()
plt.title("Esboço Gráfico das Funções")
plt.grid(True)
plt.show()
# Estimativa inicial de U a partir do gráfico
U = 3.3 # Escolhido grosseiramente pela interseção
# Passo 3: Resolver θ e encontrar x
theta = solve_theta(U)
x_aprox = theta + U
x_ref = 3.381293824 # Valor de referência
erro_relativo = abs((x_aprox - x_ref) / x_ref) * 100
# Exibir os resultados
print(f"Valor aproximado de x usando SAAMM: {x_aprox:.6f}")
print(f"Erro relativo: {erro_relativo:.2f}%")
Conclusão
O método SAAMM oferece uma abordagem simples e estruturada para resolver problemas complexos. Sua principal vantagem está na substituição da variável x por uma soma controlada (θ+U), permitindo a expansão de funções transcendentais em torno de θ. Isso simplifica significativamente a obtenção de soluções aproximadas. Além disso, o ajuste gráfico fornece uma precisão prática, mantendo a simplicidade do processo. Como um benefício adicional, o método permite refinar iterativamente o valor de x, alcançando um erro relativo dentro da precisão necessária para cada aplicação desejada.
Aplicações práticas para esse problema
Embora a equação \(2x – 7 = \sin(x)\) não pareça, à primeira vista, surgir diretamente de problemas físicos ou de engenharia tradicionais, ela pode ser uma idealização ou uma simplificação de um problema maior. Aqui estão algumas ideias onde uma equação como essa poderia aparecer: SAIBA MAIS…
1. Oscilações Não-Lineares em Física
- Contexto: A equação pode surgir ao modelar um sistema oscilatório com forças não-lineares. Por exemplo, um sistema oscilatório forçado, onde o termo \(\sin(x)\) representa uma força restauradora não linear, e \(2x – 7\) corresponde a forças externas ou amortecimento proporcional à posição.
- Exemplo Prático: Modelagem de pêndulos com pequenas perturbações externas, em que o deslocamento do pêndulo precisa equilibrar forças restauradoras e resistências externas.
2. Engenharia Elétrica: Sistemas de Circuitos Não Lineares
- Contexto: Na análise de circuitos elétricos, x poderia representar a corrente ou a tensão em um componente, e \(2x – 7\) poderia ser o comportamento aproximado de uma fonte dependente. O termo \(\sin(x)\) pode surgir de uma resposta senoidal de componentes como diodos ou indutores.
- Exemplo Prático: Um circuito contendo uma fonte dependente de tensão/corrente que gera uma resposta senoidal.
3. Termodinâmica ou Transferência de Calor
- Contexto: Em transferência de calor, x poderia ser a temperatura em um ponto específico, com \(2x−7 \) representando o fluxo de calor e \(\sin(x)\) surgindo de um modelo não linear de perda ou geração de calor.
- Exemplo Prático: Um sistema com fontes de calor oscilantes ou perdas não-lineares devido a radiação.
4. Controle e Sistemas Dinâmicos
- Contexto: Em controle de sistemas, a equação pode descrever um ponto de equilíbrio onde a força controladora \((2x – 7) \) se iguala a uma resposta não linear \((\sin(x)).\)
- Exemplo Prático: Ajuste do controle de um robô que precisa compensar uma força restauradora oscilante (como atrito não-linear ou interferências).
5. Problemas de Mecânica: Modelagem Idealizada
- Contexto: Em mecânica, a equação pode representar o equilíbrio de forças em um sistema onde uma força não-linear (como atrito ou resistência do ar) é proporcional ao seno de um deslocamento ou ângulo.
- Exemplo Prático: O movimento de uma mola ou sistema elástico submetido a uma força externa proporcional ao deslocamento e uma resistência senoidal.
Esses exemplos mostram como a equação \(2x – 7 = \sin(x)\) pode surgir como parte de um modelo idealizado ou simplificado de problemas reais. Ao resolver equações como essa, muitas vezes ganhamos insights sobre o comportamento qualitativo dos sistemas, mesmo que a modelagem completa exija mais variáveis e equações.
Vitrine dos nossos Livros
Visite nosso Blog
De Lâmpadas a Gás à Automação: A Eterna Dança da “Destruição Criativa” no Mercado de Trabalho
De Lâmpadas a Gás à Automação: A Eterna Dança da “Destruição Criativa” no Mercado de…
📘 Resolvendo com SAAMM a equação cúbica: $$x^3 – 6x^2 + 11x – 6 = 0 $$
O lugar de cada coisa: Homem x Máquina
Na ciência e na engenharia, estamos cercados por equações que precisam ser resolvidas. Mas nem…
Qual a previsão da IA daqui a uma década na vida das pessoas?
A Inteligência Artificial (IA) está evoluindo rapidamente e, em 10 anos, é provável que ela…
A IA é apenas o piano
A IA é apenas uma tecnologia poderosa, mas, como qualquer ferramenta, seu impacto depende de…
“Download” de Conhecimento: Um Mito da Era Digital
“Download” de Conhecimento: Um Mito da Era Digital Capacidade de Processamento: É comum que as…