O método gráfico é uma técnica visual simples, mas poderosa, para encontrar uma estimativa inicial aproximada da raiz de uma equação. Apesar da simplicidade do método, ele pode ser um ponto de partida extremamente útil para estratégias mais avançadas de determinação de raízes.
Para o problema em questão, em que se deseja encontrar qual o volume, V, que corresponde à pressão, P = 22.5 atm, vamos plotar a função de Van der Waals mostrada abaixo:
$$ f = a_{v} V^3+b_v V^2 + c_v V + d_v $$
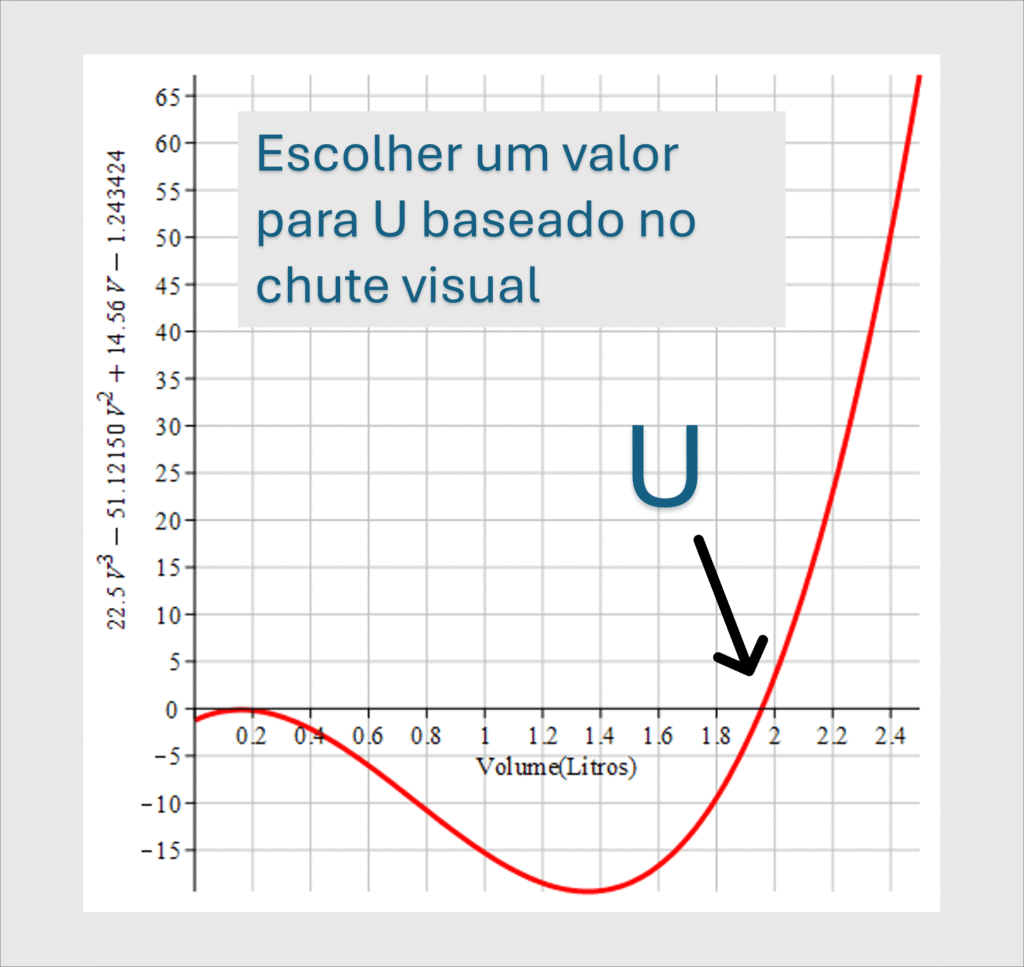
Observando o gráfico podemos arbitrar, U = 1.95.
Veja como podemos obter o gráfico no Maple
Código Maple para realização do gráfico
restart;
##############################
P := 22.5:
n := 2;
a := 3.64;
b := 0.0427;
T := 300;
R := 0.082;
##############################
av := P;
bv := -P*b*n - R*T*n;
cv := a*n^2;
dv := -a*n^3*b;
##############################
f := V^3*av + V^2*bv + V*cv + dv;
##############################
plot(f, V = 0 .. 2.5, axes = normal, labels = ["Volume(Litros)", f], axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"], style = [line], symbol = [circle], color = [red], thickness = [3]);
Com o valor de U estimado, U = 1.95, podemos agora usar a expressão calculada para \(\theta\) e obter \( V = \theta + U\):
$$ V = \frac {-(U^3 a_v + U^2 b_v+c_v U+ d_v)} {3 U^2 a_v + 2 U b_v+c_v} +U$$
O valor obtido foi: V = 1.955653620.
theta := -(U^3*av + U^2*bv + U*cv + dv)/(3*U^2*av + 2*U*bv + cv);
V := theta + U;
U := 1.95;
V;
1.955653620
O valor de referência pode ser calculado no Maple, e forneceu:
$$ V = 1.955618200$$
Com isso podemos tambem calcular o erro relativo, que no caso foi:
$$ E_r = 0.0018 \% $$
solve({22.5*Vn^3 - 51.12150*Vn^2 + 14.56*Vn - 1.243424 = 0}, {Vn});
{Vn = 1.955618200}
#########################
Vn := 1.955618200;
Er := abs((Vn - V)/Vn)*100;
Er := 0.001811191980 %
## Como vemos, o erro relativo obtido é bem baixo, e pode ser usado em várias situações. De fato, sua usabilidade deve ser analisada caso a caso.
Resposta: (a) Com o uso do Método SAAMM, o volume aproximado obtido foi de V = 1.955618200 litros quando a pressão P = 22.5 atm, e apresentou um erro relativo de 0.0018 %.
