Neste caso, vamos aplicar a metodologia desenvolvida para resolver a equação cúbica de Van der Waals no intervalo de pressões [Pini, Pfin], usando uma única aproximação linear para U = U(P). Essa abordagem simplificada, com m=1, é um primeiro passo para compreender o comportamento da função V(P) e avaliar sua precisão.
1. A Equação e a Abordagem Gráfica
A equação cúbica de Van der Waals é escrita como:
a(P) V3+ b(P) V2 + c(P) V + d(P) = 0,
onde os coeficientes a(P), b(P), c(P), e d(P) dependem dos parâmetros do gás e da pressão P.
Primeiramente, o método gráfico foca em aproximar U, um ponto de referência para resolver a equação de Van der Waals. Paralelamente, adotamos a estratégia de dividir o intervalo de P em partes (neste caso apenas uma (m = 1)) e aproximar U(P) por uma função linear.
2. Parametrização de U(P) com m = 1
Com m = 1, o intervalo de pressão [Pini, Pfin] não é dividido em subintervalos, e U(P) é descrito por uma única função linear:
U(P)=a1P+b1,
onde a1 e b1 são determinados pelos valores de U nos extremos do intervalo: U(Pini)=U1, U(Pfin)=U2.
Os coeficientes são calculados como:
a1 = (U2 − U1)/(Pfin − Pini), b1 = U1 − a1Pini.
3. Implementação e Resultados
3.1 Valores de Pressão e Volumes Extremos
Tomamos Pini=5 atm e Pfin=40 atm. Os volumes correspondentes são obtidos resolvendo a equação cúbica numericamente: U1=9.63 L, U2=0.97 L.
3.2 Cálculo dos Coeficientes de U(P)
a1 = (U2−U1)/(Pfin−Pini) = (0.97−9.63)/(40−5) = −0.2457,
b1=U1−a1Pini =9.63−(−0.2457⋅5)=10.86.
A aproximação de U(P) torna-se:
U(P)=−0.2457P+10.86.U(P).
Acompanhe os resultados que obtivemos no Maple.

Inicialmente, fornecemos as constantes do problema; resolvemos numericamente a equação de Van der Waals, para termos uma referência para calcularmos, na etapa final, o erro relativo, e criamos uma forma de calcular as pressões nos subintervalos, em função de m.
DeltaP := m -> (Pm - P1)/m:
Pressures := m -> local i; [seq(P1 + (i - 1)*DeltaP(m), i = 1 .. m + 1)]
Como neste caso, m = 1, temos P1 = Pini e P2 = Pfin. Embora, aqui pareça sem sentido, à medida que m aumenta, esse procedimento pode se tornar muito útil. Embora, tambem, o desenvolvedor do trabalho possa usar uma outra estratégia, para encontrar um valor ótimo de Pk para minimizar o erro relativo. Aqui vamos explorar esse caminho mais simples, e deixamos para o desenvolvedor criar suas próprias estratégias de otimização.
Em seguida, temos que estimar os valores de U1 e U2, correspondentes as pressões, P1 e P2, para construirmos a aproximação, U = U(P). Normalmente, usaríamos um método gráfico para fazer isso, e chutarmos valores para U1 e U2. Todavia, aqui, somente para simplificar esse processo, e nos concentrar naquilo que estamos interessados neste projeto, vamos usar a ferramenta fsolve do Maple, para nos dar esses valores, mais rapidamente. Com isso, podemos obter, ak e bk, e finalmente,
U = akP + bk.
θ = -bk/ak.
No caso, k = 1.
Tendo encontrado θ, podemos agora obter:
V := P -> theta(P) + U(P)
Conhecendo-se a aproximação, V = V(P), podemos fazer o gráfico comparativo no Maple, das curvas do volume exato, Vex, a aproximação, U = U(P), e o valor aproximado, V = V(P).

A observação do gráfico confirma que a aproximação inicial de U(P), representada pela linha preto pontilhada, fornece uma estimativa inicial simplificada, mas relativamente grosseira para o problema. Já o resultado em azul, correspondente ao modelo SAAMM com m=1, é visivelmente mais alinhado com o comportamento esperado para Vex, mas ainda apresenta erros relativos consideráveis.
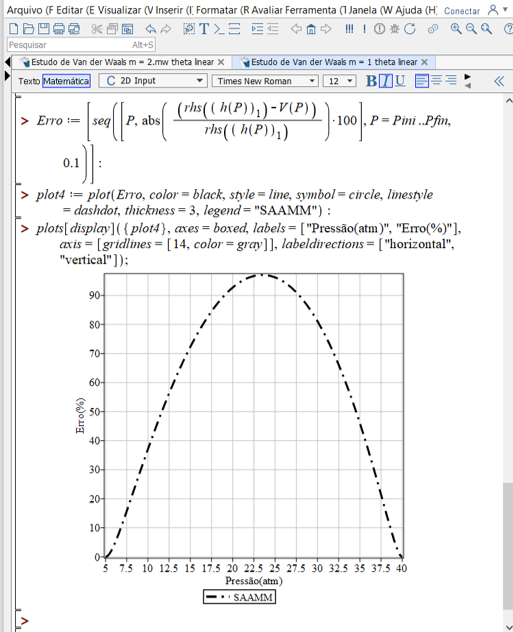
O método SAAMM demonstra um comportamento convergente, no qual o resultado pode ser iterativamente refinado. Ao atualizar U(P) com os valores obtidos de V(P) em uma iteração anterior, a solução se ajusta progressivamente, reduzindo significativamente o erro em poucos passos.
Mas, se não quisermos usar a estratégia de iteratividade, particionar U(P) em múltiplos subintervalos — permitindo que U(P) seja descrito como uma função piecewise linear — é essencial. Esse método possibilita capturar melhor as variações não-lineares de V(P) em relação a P, promovendo uma redução significativa no erro relativo e melhorando a convergência do modelo SAAMM.
Vejamos a seguir os resultados quando fazemos, m = 2 (…->).
- Para m=1: Linearização única no intervalo inteiro, maior erro. (…->)
- Para m=2: Melhor aproximação com dois segmentos. (…->)
- Para m=3: Refinamento ainda maior, com possibilidades de erro relativo no resultado final, significativamente reduzido. (…->)
- Assim por diante. Generalização para m. (…->)
- Generalização para m com ajuste parabólico. (…->)
