Resolvendo com SAAMM a equação cúbica de Van der Waals: $$ a_{v} V^3+b_v V^2 + c_v V + d_v =0 $$

Resolvendo com SAAMM a equação cúbica de Van der Waals:

$$ a_{v} V^3+b_v V^2 + c_v V + d_v =0 $$

A Equação de Van der Waals

A equação de Van der Waals é uma modificação da lei dos gases ideais, que busca descrever o comportamento de gases reais, considerando as forças intermoleculares e o volume finito das moléculas. Ela é representada pela Equação (1) dada por:

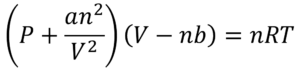
Onde:

P: Pressão
V: Volume
n: Número de moles
R: Constante universal dos gases (0,082 (atm x L x mol^-1 x K^-1))
T: Temperatura
a e b: Constantes características de cada gás

Problema: Um cilindro contém 2 moles de CO₂ a uma temperatura de 300 K. As constantes de Van der Waals para o CO₂ são: a = 3.64 L² atm/mol² e b = 0.0427 L/mol. Nestas condições, determine:

(a) O volume, V, ocupado pelo gás quando a pressão no cilindro é P = 22.5 atm (Utilize o método SAAMM).

Solução:

Ao rearranjar a Eq. (1) de modo a buscar a dependência no volume em função da pressão, chegamos à expressão abaixo:

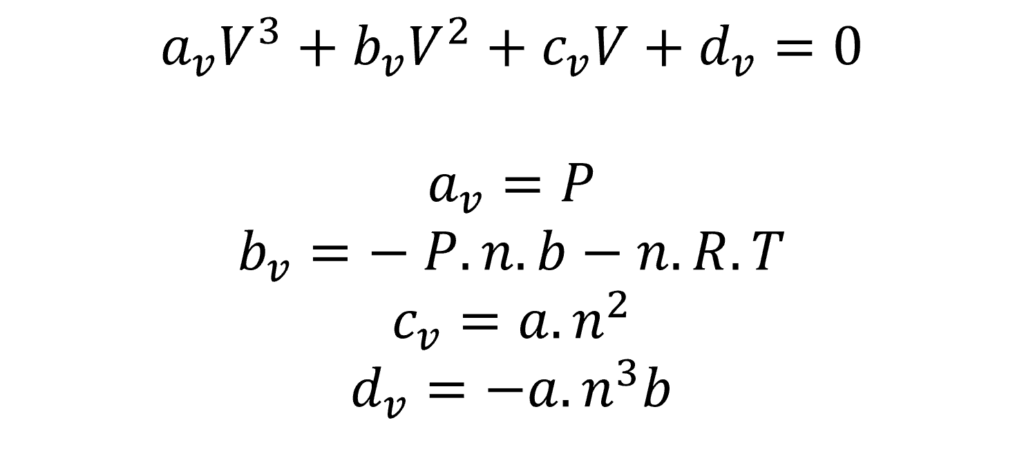
Se quiser, veja aqui como obtemos esses resultados.

Como sabemos, lidar com uma equação cúbica é complicado. Então, vamos a seguir demonstrar como o método SAAMM nos permite abordar esse problema de uma forma mais simples. Basicamente, o Método SAAMM é composto, neste caso, por três passos:

O Método

Passo 1 : Mudança de Variável: Aplicar o Método SAAMM a este problema consiste em substituir a variável de interesse, V, por, V = θ + U. Isso permite reorganizar a equação para um formato mais simples e mais tratável. (… ->)

Passo 2: Linearização em θ: Ao trabalhar com θ, desprezando os termos de ordens superiores, cria-se uma equação simplificada que ainda captura a essência do problema. Isso facilita uma solução analítica. (…->)

Passo 3: Uso do Método Gráfico: A obtenção de U como um chute inicial (mesmo que grosseiro) complementa perfeitamente a abordagem analítica, fornecendo a base para refinamentos iterativos, se necessário. (…->)

Resposta: (a) Com o uso do Método SAAMM, o volume aproximado obtido foi de V = 1.955618200 litros quando a pressão P = 22.5 atm, e apresentou um erro relativo de 0.0018 %.

(b) Obtenha o gráfico de V(P) x P, considerando o intervalo de pressões, 5 atm <= P <= 40 atm.

Solução:

No item (a), calculamos o volume, V, para a pressão P = 22.5 atm, usando o método gráfico. Resumidamente, plotamos a função de Van der Waals:

$$ f_{VW} (V)= a_{v} V^3+b_v V^2 + c_v V + d_v $$

Para essa pressão, determinamos o valor do chute inicial U por meio da análise gráfica. Conhecido U, aplicamos a fórmula:

$$\theta = -\frac{(U^3 av + U^2 bv + U cv + dv)}{(3U^2 av + 2 U bv + cv)} $$

e, em seguida, obtemos:

$$V= \theta + U$$

Neste caso, encontramos V = 1.955653620 Litros.

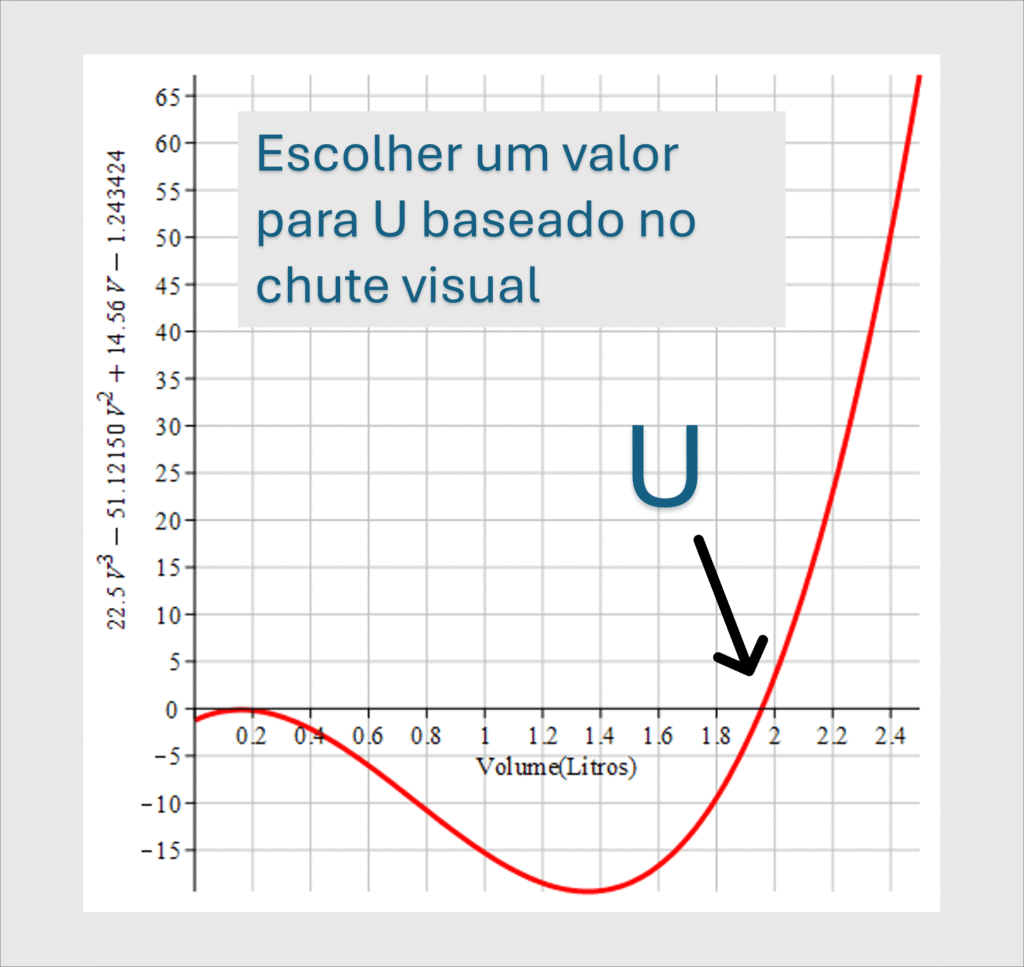
Veja como podemos obter o gráfico no Maple

Código Maple para realização do gráfico

restart;
##########################
P := 22.5;
n := 2;
a := 3.64;
b := 0.0427;
T := 300;
R := 0.082;

##########################
av := P;
bv := -P*b*n - R*T*n;
cv := a*n^2;
dv := -a*n^3*b;
##########################

f := V^3*av + V^2*bv + V*cv + dv;               

plot(f, V = 0 .. 2.5, axes = normal, labels = ["Volume(Litros)", f], axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"], style = [line], symbol = [circle], color = [red], thickness = [3]);

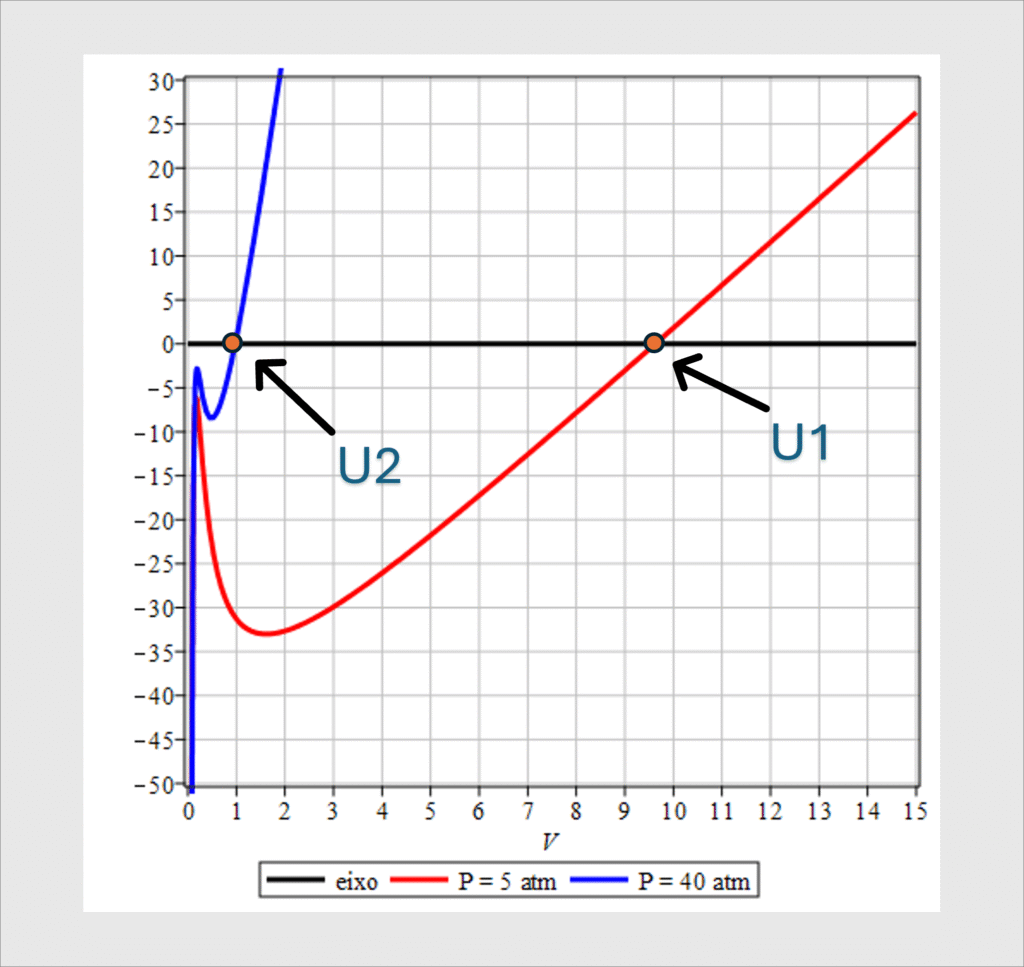
O gráfico ao lado mostra os valores de U, para dois pontos distintos de pressão, P1 = 5 atm e P2 = 40 atm. Observando esse gráfico, vemos que U varia amplamente nesse intervalo, e podemos concluir que U não é uma constante, mas sim, é uma função da pressão, P.

Então, propomos investigar um ajuste linear, escrevendo uma função U = U(P) tomando os dois pontos da extremidade do intervalo, 5 atm <= P <= 40 atm, assim P1 = 5 atm e P2 = 40 atm. O gráfico ao lado mostra as duas curvas para a função de Van der Waals com P1 = 5 atm e P2 = 40 atm, sendo, respectivamente, U1 = 9.5 e U2 = 1, estimativas visuais.

Veja como podemos obter o gráfico no Maple

Código Maple para realização do gráfico

restart;
#######################
n := 2;
a := 3.64;
b := 0.0427;
T := 300;
R := 0.082;
#######################
av := P -> P;
bv := P -> -P*n*b - n*R*T;
cv := a*n^2;
dv := -a*n^3*b;
#######################
fesq := P -> (P + a*n^2/V^2)*(-b*n + V);
fdir := n*R*T;
#######################
P1 := 5;
P2 := 40;

plot1 := plot(fesq(P1) - fdir, V = 0 .. 15, color = red, legend = "P = 5 atm");
plot2 := plot(fesq(P2) - fdir, V = 0 .. 15, color = blue, legend = "P = 40 atm");
plot3 := plot(0, V = 0 .. 15, color = black, legend = "eixo");

plots[display]({plot1, plot2, plot3}, axes = boxed, axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"], thickness = [3, 3, 3], view = [0 .. 15, -50 .. 30]);

Com os dois pontos escolhidos, (P1 = 5 atm, U1 = 9.5 litros) e (P2 = 40 atm, U2 = 1 litro) podemos buscar um ajuste linear para esse valores, de tal modo que, podemos escrever:

$$U(P) = a_{k1}P + b_{k1}, $$

com $a_{k1} = \frac {(U_1 – U_2)} {(P_1 – P_2)} e b_{k1} = \frac{(P_1 U_2 – P_2 U_1)}{(P_1 -P_2)}$

Analogamente ao já realizado anteriormente,

$$V(P) = \theta(P) + U(P)$$

$$V(P) = -\frac {U(P)^3 a_v(P) +U(P)^2 b_v(P) + c_v U(P) + d_v}{3 U(P)^2 a_v(P) + 2 U(P) b_v(P) + c_v} + U(P)$$

Veja como podemos obter o gráfico no Maple

Código Maple para realização do gráfico

restart;
#######################
n := 2;
a := 3.64;
b := 0.0427;
T := 300;
R := 0.082;
#######################
av := P -> P;
bv := P -> -P*n*b - n*R*T;
cv := a*n^2;
dv := -a*n^3*b;
#######################
fesq := P -> (P + a*n^2/V^2)*(-b*n + V);
fdir := n*R*T;
#######################
P1 := 5;
P2 := 40;

plot1 := plot(fesq(P1) - fdir, V = 0 .. 15, color = red, legend = "P = 5 atm");
plot2 := plot(fesq(P2) - fdir, V = 0 .. 15, color = blue, legend = "P = 40 atm");
plot3 := plot(0, V = 0 .. 15, color = black, legend = "eixo");

plots[display]({plot1, plot2, plot3}, axes = boxed, axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"], thickness = [3, 3, 3], view = [0 .. 15, -50 .. 30]);

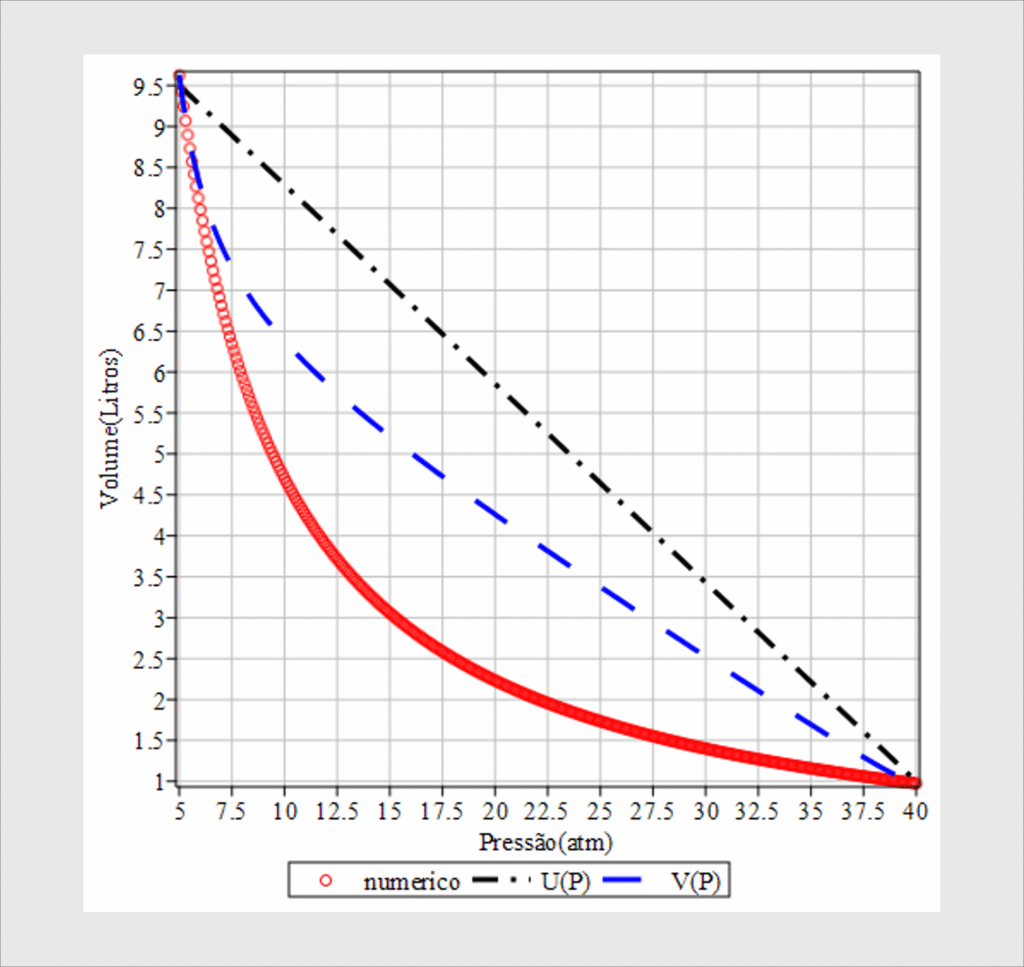
Utilizando os resultados acima, obtemos o gráfico ao lado, onde vemos a comparação entre o resultado numérico esperado, em vermelho, e o resultado fornecido pelo modelo analítico aproximado em azul. Note que U(P), o chute inicial, é a linha em preto. Comparando a linha em preto e a linha e azul, notamos uma melhora significativa do chute inicial, pois encontra-se mais próxima da linha vermelha que corresponde ao resultado numérico esperado.

Veja como podemos obter o gráfico no Maple

Código Maple para realização do gráfico

restart;
#########################
n := 2;
a := 3.64;
b := 0.0427;
T := 300;
R := 0.082;
#########################
av := P -> P;
bv := P -> -P*n*b - n*R*T;
cv := a*n^2;
dv := -a*n^3*b;
#########################
fesq := P -> (P + a*n^2/V^2)*(-b*n + V);
fdir := n*R*T;
#########################
P1 := 5;
P2 := 40;
plot1 := plot(fesq(P1) - fdir, V = 0 .. 15, color = red, legend = "P = 5 atm");
plot2 := plot(fesq(P2) - fdir, V = 0 .. 15, color = blue, legend = "P = 40 atm");
plot3 := plot(0, V = 0 .. 15, color = black, legend = "eixo");
plots[display]({plot1, plot2, plot3}, axes = boxed, axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"], thickness = [3, 3, 3], view = [0 .. 15, -50 .. 30]);

#########################
h := P -> fsolve({av(P)*Vex^3 + bv(P)*Vex^2 + cv*Vex + dv = 0}, {Vex});
#########################
dados := [seq([P, rhs(h(P)[1])], P = 5 .. 40, 0.1)];

#########################
P1 := 'P1';
P2 := 'P2';
hu1 := solve({U1 = P1*ak1 + bk1, U2 = P2*ak1 + bk1}, {ak1, bk1});
                  
#########################

ak1 := (U1 - U2)/(P1 - P2);
bk1 := (P1*U2 - P2*U1)/(P1 - P2);
#########################
P1 := 5;
P2 := 40;
#########################
U1 := 9.5;
U2 := 1.0;
#########################
U := P -> ak1*P + bk1;   
#########################
a1 := P -> 3*U(P)^2*av(P) + 2*U(P)*bv(P) + cv;
b1 := P -> U(P)^3*av(P) + U(P)^2*bv(P) + cv*U(P) + dv;
theta := P -> -b1(P)/a1(P);
#########################
V := P -> theta(P) + U(P);                         
#########################
plot1 := plot(dados, color = red, style = point, symbol = circle, linestyle = dot, thickness = 3, legend = "numerico");
plot2 := plot(V(P), P = P1 .. P2, color = blue, style = line, symbol = point, linestyle = spacedash, thickness = 3, legend = "V(P)");
plot3 := plot(U(P), P = P1 .. P2, color = black, style = line, symbol = point, linestyle = dashdot, thickness = 3, legend = "U(P)");
plots[display]({plot1, plot2, plot3}, axes = boxed, labels = ["Pressão(atm)", "Volume(Litros)"], axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"]);

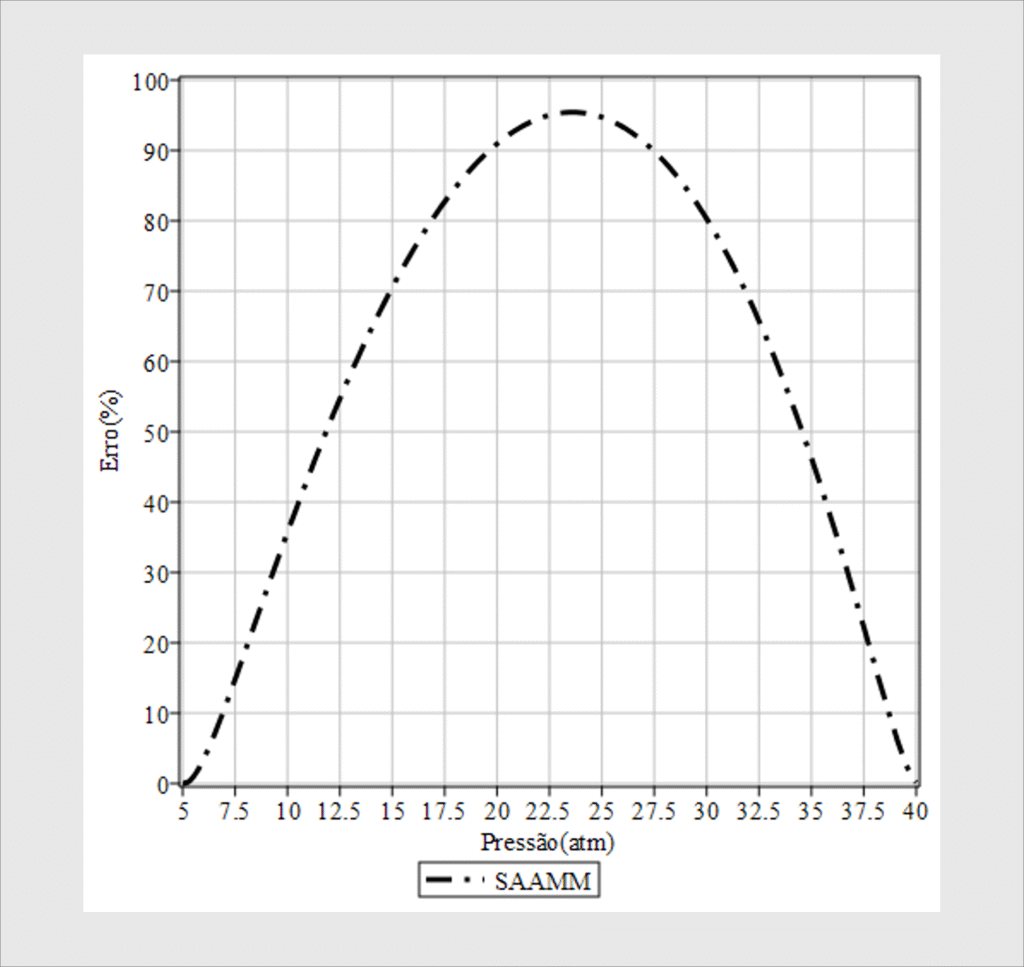
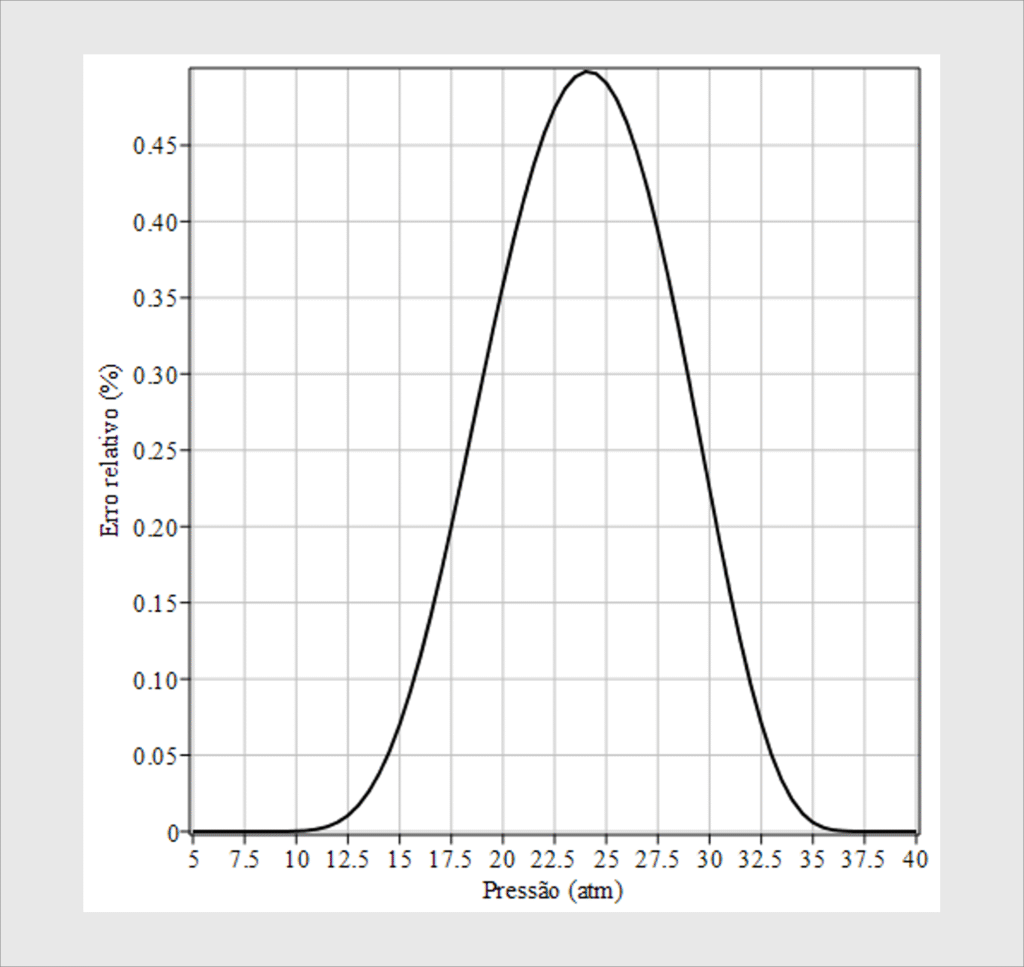
O gráfico do erro relativo é mostrado na figura ao lado. Este resultado está muito ruim, todavia, nos serve como uma pista do que podemos fazer em seguida no sentido de melhorar a precisão dos resultados. Uma das grandes vantagens do Método SAAMM está em sua capacidade de refinar iterativamente a solução. A ideia é simples:

usamos o valor obtido de V(P) como uma nova estimativa para U(P);
recalculamos $\theta$ e obtemos um novo valor para V(P);
repetimos esse processo algumas vezes, até que a solução esteja aceitável.

Veja como podemos obter o gráfico no Maple

Código Maple para realização do gráfico

Erro := [seq([P, 100*abs((rhs(h(P)[1]) - V(P))/rhs(h(P)[1]))], P = P1 .. P2, 0.1)];
plot4 := plot(Erro, color = black, style = line, symbol = circle, linestyle = dashdot, thickness = 3, legend = "SAAMM");
plots[display]({plot4}, axes = boxed, labels = ["Pressão(atm)", "Erro(%)"], axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"], view = [P1 .. P2, 0 .. 100]);

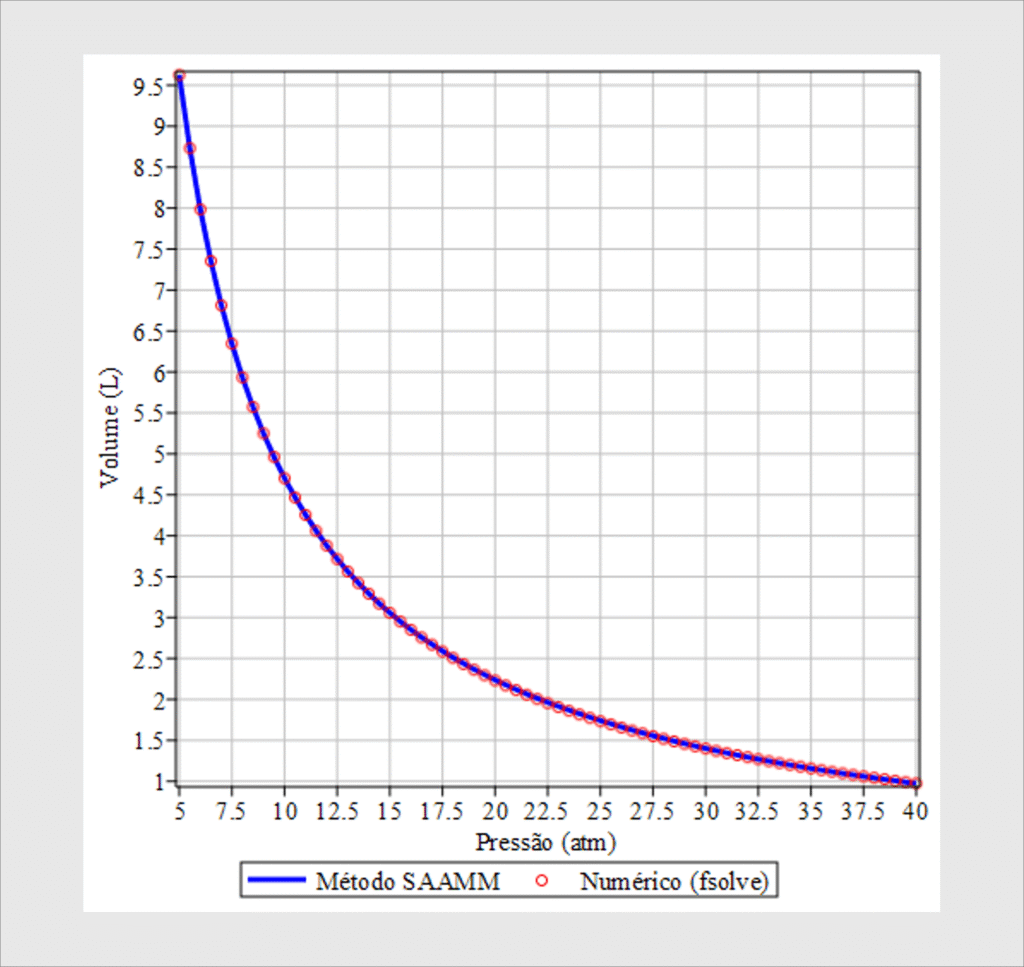
Resposta: (b) Com o uso do Método SAAMM, obtivemos o gráfico, V(P) x P.

Após apenas 5 iterações, os valores de V(P) já apresentam uma excelente concordância com a solução numérica obtida pelo fsolve, no Maple. Isso mostra a eficiência e robustez do método.

Por que o SAAMM é vantajoso? Comparando o SAAMM com os métodos tradicionais.

🔹 Método de Newton
- Precisa de uma boa aproximação inicial próxima da raiz.
- Pode divergir se o chute não for adequado.
- Exige o cálculo explícito da derivada da função.
🔹 Método da Bisseção
- É garantido que converge, mas de forma lenta.
- Depende de ter um intervalo onde a função muda de sinal.
- Não fornece diretamente uma aproximação analítica, apenas refinamento numérico.
🔹 Método SAAMM
- Trabalha de forma analítica aproximada, permitindo obter expressões simples para V(P).
- O chute inicial U(P) pode ser grosseiro; mesmo assim, o método refina rapidamente.
- Não exige conhecer intervalos de mudança de sinal (como a bisseção) nem precisão inicial (como Newton).
- Em poucas iterações (5 foram suficientes aqui), atinge um erro muito baixo.

Veja o código Maple completo para obtenção do gráfico V(P) x P

Código no Maple

restart;
n := 2;
a := 3.64;
b := 0.0427;
T := 300;
R := 0.082;
num_iteracoes := 5;
av := P -> P;
bv := P -> -P*n*b - n*R*T;
cv := a*n^2;
dv := -a*n^3*b;
h := P -> fsolve({av(P)*Vex^3 + bv(P)*Vex^2 + cv*Vex + dv = 0}, {Vex});
dados := [seq([P, rhs(h(P)[1])], P = 5 .. 40, 0.5)];
P1 := 5;
P2 := 40;
U1 := 9.5;
U2 := 1.0;
ak1 := (U1 - U2)/(P1 - P2);
bk1 := (P1*U2 - P2*U1)/(P1 - P2);
U := P -> ak1*P + bk1;
a1 := (P, U) -> 3*U^2*av(P) + 2*U*bv(P) + cv;
b1 := (P, U) -> U^3*av(P) + U^2*bv(P) + U*cv + dv;
theta := (P, U) -> -b1(P, U)/a1(P, U);
V := proc(P) local Uant, Uprox, Vaprox, k; Uant := U(P); for k to num_iteracoes do Vaprox := theta(P, Uant) + Uant; Uprox := Vaprox; Uant := Uprox; end do; return Vaprox; end proc;
plot1 := plot(dados, color = red, style = point, symbol = circle, linestyle = dot, thickness = 3, legend = "Numérico (fsolve)");
plot2 := plot([seq([P, V(P)], P = 5 .. 40, 0.5)], color = blue, style = line, thickness = 3, legend = "Método SAAMM");
plots[display]({plot1, plot2}, axes = boxed, labels = ["Pressão (atm)", "Volume (L)"], axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"]);
Erro := [seq([P, 100*abs((rhs(h(P)[1]) - V(P))/rhs(h(P)[1]))], P = 5 .. 40, 0.5)];
plot3 := plot(Erro, color = black, style = line, thickness = 2, axes = boxed, labels = ["Pressão (atm)", "Erro relativo (%)"], axis = [gridlines = [14, color = gray]], labeldirections = ["horizontal", "vertical"]);

✅ Resumo Didático:

Definimos a cúbica de Van der Waals.
Usamos fsolve como referência.
Construímos o método SAAMM:
- Chute inicial U(P).
- Correção θ(P,U).
- Iterações sucessivas até convergir.
Comparamos SAAMM × numérico e mostramos o erro.

Explicação do Código:

restart; → limpa a memória do Maple.

n, a, b, T, R → são os parâmetros do problema (número de mols, constantes de Van der Waals, temperatura e constante dos gases).

num_iteracoes := 5; → define quantas iterações do método SAAMM serão realizadas (quantidade suficiente para boa precisão).

av(P) → depende da pressão.

bv(P) → depende da pressão, do número de mols e da temperatura.

cv e dv → constantes fixas para o gás considerado.

Aqui usamos o fsolve (método numérico do Maple) para resolver a cúbica diretamente.

dados → gera os pares (P, V) no intervalo de pressão de 5 a 40 atm, que serão usados como comparação.

O método SAAMM parte de U(P) como aproximação inicial.

Pegamos duas condições de contorno (pressões extremas) e fazemos uma interpolação linear para U.

Assim, para qualquer pressão P, temos um chute inicial para U.

θ é obtido ao aplicar a linearização do SAAMM.

a1 e b1 vêm da expansão da cúbica em torno de U.

$\theta(P, U)$ fornece a correção que será somada ao U para melhorar a aproximação do volume.

Aqui está o coração do método:

Começamos com Uant = U(P) (chute inicial).
Em cada iteração, calculamos: V=θ(P,Uant)+UantV = \theta(P, Uant) + UantV=θ(P,Uant)+Uant
Atualizamos Uant com esse novo valor.

Após 5 iterações (num_iteracoes = 5), temos um valor de volume V(P) muito próximo do verdadeiro.

plot1 → resultado numérico (fsolve).

plot2 → resultado aproximado do SAAMM.

Ambos são sobrepostos no mesmo gráfico para comparação.

Calcula o erro relativo (%) entre o resultado numérico (fsolve) e o obtido pelo SAAMM.

Mostra graficamente que mesmo com apenas 5 iterações, o método já fornece um erro muito pequeno.

✅ Resumo Didático:

Definimos a cúbica de Van der Waals.
Usamos fsolve como referência.
Construímos o método SAAMM:
- Chute inicial U(P).
- Correção θ(P,U).
- Iterações sucessivas até convergir.
Comparamos SAAMM × numérico e mostramos o erro.

Assim, o SAAMM combina intuição matemática com eficiência computacional, sendo uma alternativa poderosa e didática para problemas como a equação cúbica de Van der Waals.

Dessa forma, mostramos como o Método SAAMM permite resolver de maneira prática e rápida um problema que, em métodos convencionais, exigiria muito mais esforço numérico.